Une géométrie non euclidienne
Présentation
A l'école, on vous a toujours appris que "Par deux points il ne passe qu'une seule droite", "La somme des angles d'un triangle vaut toujours 180 degrés" ?Eh bien, préparez vous, vous allez voir que ce n'est pas forcément vrai. En effet, personne n'a jamais réussi à démontrer la première propriété : Par deux points il ne passe qu'une seule droite. Dès lors, de nombreux mathématiciens ont essayé de créer des géométries qui ne respecte pas cette propriété, un des axiomes d'Euclide, et cela a aboutit à la création de la géométrie sphérique.
Imaginez que le petit prince, sur sa petite planète de 12 mètres de rayon, veuille faire de la géométrie. Lorsqu'il trace une droite, celle-ci sera en réalité courbe. En réalité, il se passe exactement la même chose sur Terre, mais nous sommes trop petits pour nous en appercevoir.
Cette géométrie, qui consiste non plus à dessiner sur une feuille de papier plane, comme on le ferait en géométrie plane, mais de dessiner les figures géométriques sur une sphère.
Quelques propriétés
Accrochez vous, voici le premier théorème de la géométrie sphérique :Theorème : Un triangle qui possède deux angles droits est un triangle isocèle.
Vous ne me croyez pas? Un triangle ne peut pas avoir deux angles droits?
Imaginez un peu : Le petit prince trace une première droite : il s'agit de l'équateur de sa planète. Puis, il trace deux droites qui lui sont parallèles, par exemple deux méridiens de sa planète. Bien sur, les deux méridiens sont perpendiculaires à l'équateur, mais ils se rejoignent aux pôles. Ainsi, un triangle formé de l'équateur et de deux méridiens sera isocèle, et possèdera deux angles droits.
Si vous ne me croyez toujours pas, voici une image pour vous en convaincre :
Vous me suivez toujours? Alors accrochez vous, voici le deuxième théorème de la géométrie sphérique :
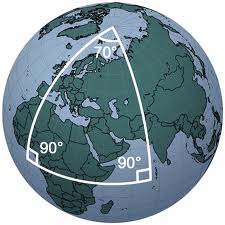
Théorème : Un triangle qui possède trois angles droits est un triangle équilatéral.
Eh oui, un triangle, en géométrie sphérique, peut avoir trois angles droits? Vous ne me croyez pas? Voyez par vous même :

NB : Rassurez vous, un triangle ne peut pas avoir quatres angles droits!!